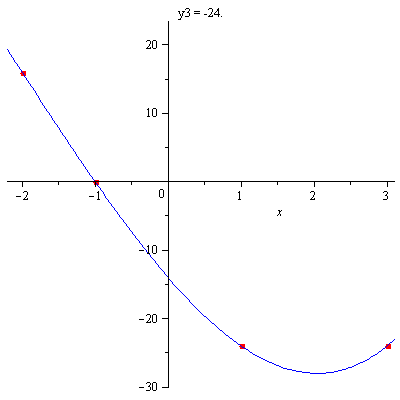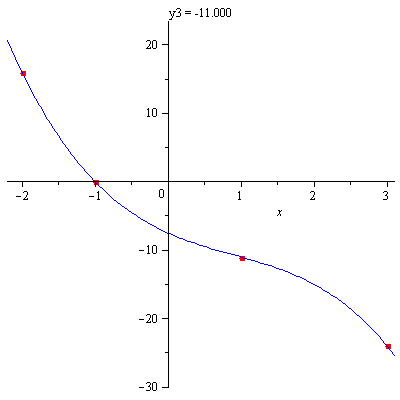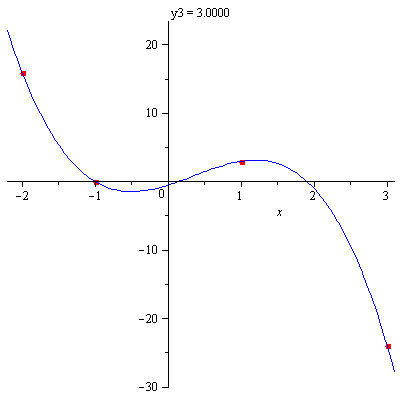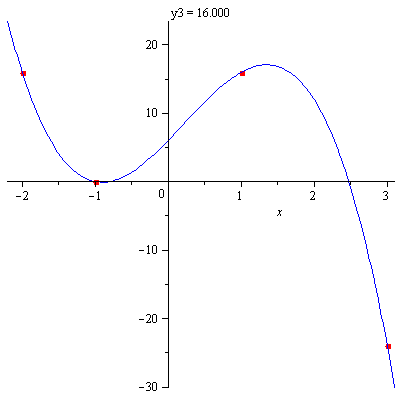|
|
Arkiv: Gamle ting og sager
Gamle forsideopgaver og illustrationer
Animation af Taylorpolynomier

Maple-kommandoerne
with(plots):
f:=x->1/(1+x^2):
q:=25:
bg:=plot(f(x),x=-1..1,thickness=3):
p1:=p->plot(mtaylor(f(x),x=0,round(2*p+1)),x=-1..1,color=blue,caption="n = 2*p"):
animate(p1,[p],p=0..q-1,frames=q,background=bg,trace=q);
Animation af polynomium gennem 4 punkter
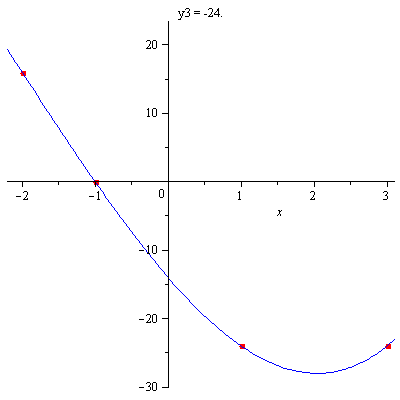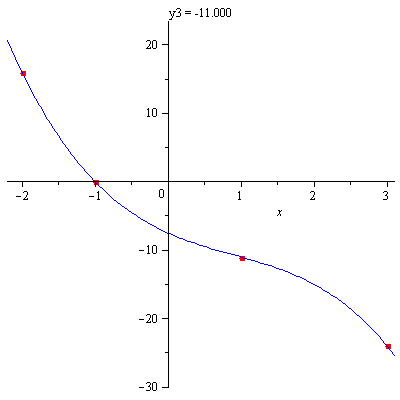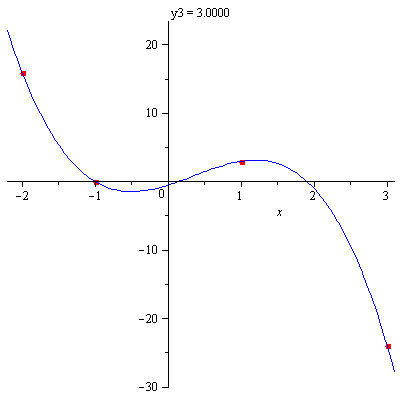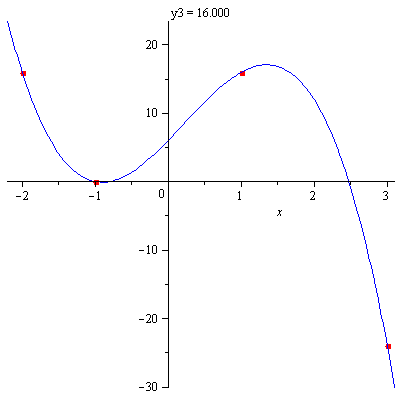
Maple-kommandoerne
Beregningen af polynomiet er naturligvis også udført i Maple, men er ikke medtaget her. Resultatet er blot tastet ind som pol nedenfor.
with(plots):
punkter:=[[-2, 16], [-1, 0], [1, y3], [3, -24]];
pol:=-2+y3/2+(5/3+7/12*y3)*x+2*x^2+(-5/3-1/12*y3)*x^3;
R:=-24..16:
FR:=41:
p1:=animate(plot,[punkter,style=point,symbol=solidcircle,symbolsize=15],y3=R,frames=FR):
p2:=animate(plot,[pol,x=-2.2..3.1,color=blue],y3=R,frames=FR):
display(p1,p2);
Animation af farver

Maple-kommandoerne
with(plots):
animate(plot,[[sin(g*x),cos(g*x)],x=0..6*Pi,color=[COLOR(RGB,1-g,g,g^2),COLOR(RGB,g,1-g,g^2)],filled=true,axes=none],g=0..1);
Komplekse tal er punkter i planen
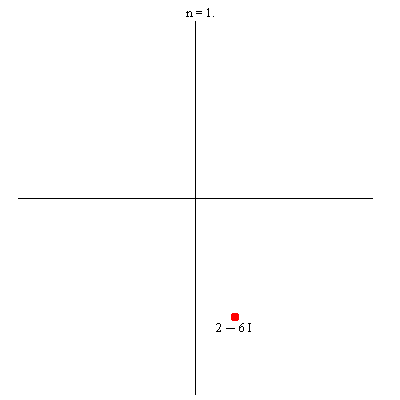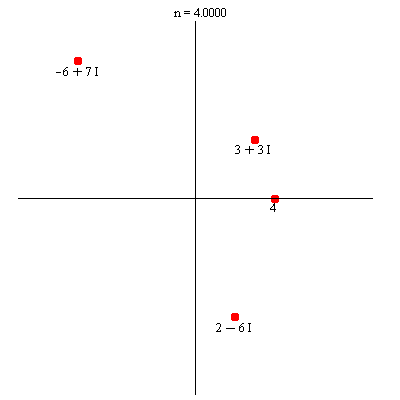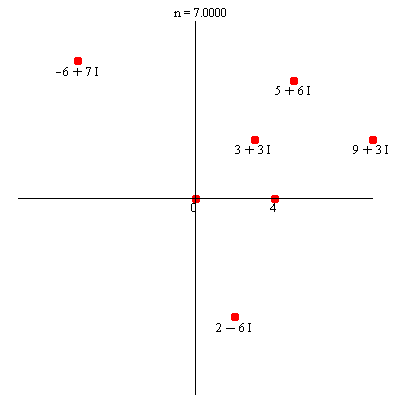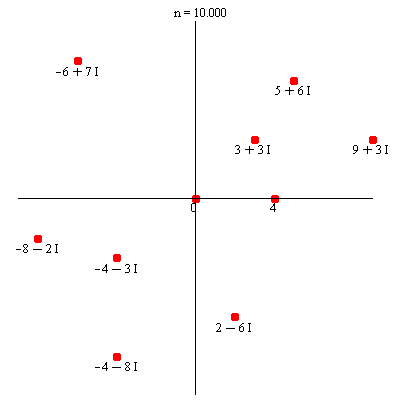
Maple-kommandoerne
with(plots):
billede:=proc(rg) local pkt,LR,p1,p2;
uses plots;
pkt:=RandomTools:-Generate(complex(integer(range=rg)));
LR:=[Re,Im-1/2,x->typeset(x)](pkt);
p1:=complexplot([pkt],rg,lhs(rg)-1..rhs(rg),style=point,
symbol=solidcircle,symbolsize=20,tickmarks=[0,0]);
p2:=textplot(LR);
display(p1,p2,scaling=constrained);
end proc:
N:=10:
animate(billede,[-9..9],n=1..N,frames=N,trace=N);
Hovedargumentet for et komplekst tal

Maple-kommandoerne
Følgende kommandoer forudsætter DMat-pakken, idet proceduren ArgumentPlot tilhører denne pakke.
with(plots):
with(DMat):
L:=remove(x->has(denom(x),12),[seq(Pi*k/12,k=0..23)]);
#
#Her blev taget vinkler, der svarer til "pæne" komplekse tal
#
animate(ArgumentPlot,[2*cos(t)+I*2*sin(t)],t=L);
Nulpunkterne for tilfældigt valgt polynomium af grad 200

Maple-kommandoerne
with(plots):
p:=RandomTools:-Generate(polynom(integer(range=-99..99),z,degree=200)):
r:=fsolve(p=0,z,complex):
f:=pkt->complexplot([pkt],style=point,symbol=solidcircle,color=COLOR(RGB,1/2+Re(pkt)/2,.3,.3),scaling=constrained):
animate(f,[pkt],pkt=[r],trace=200);
Nulpunkterne for 25 tilfældigt valgte polynomier
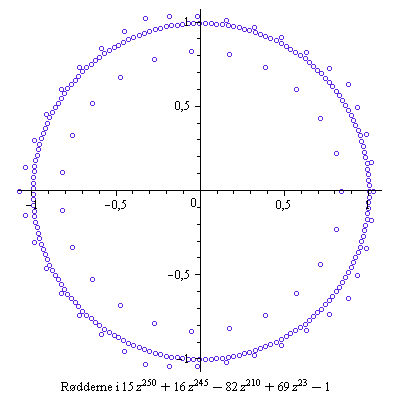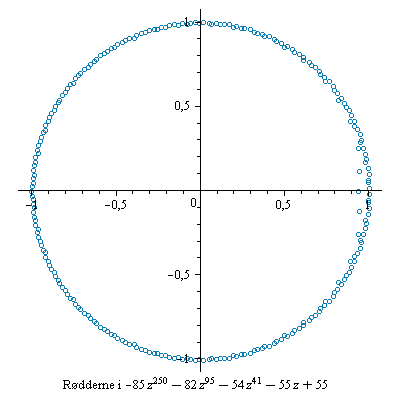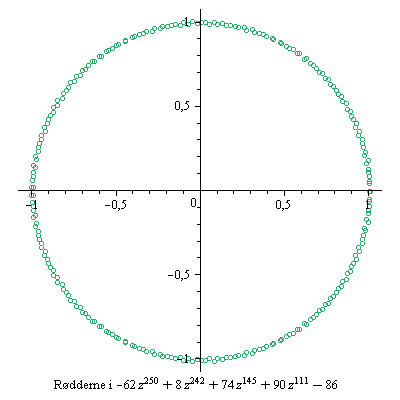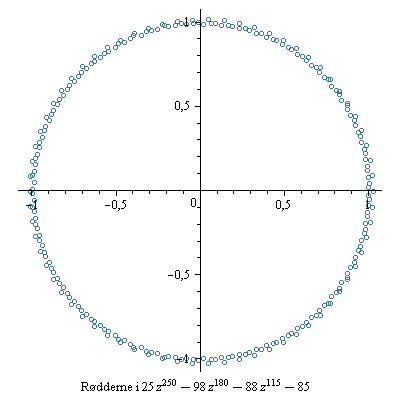
Polynomierne er alle af grad 250, men indeholder kun 5 led.
Koefficienterne er tilfældigt valgte hele tal mellem -99 og 99.
Maple-kommandoerne
with(plots):
rd:=rand(-99..99):
rc:=evalf@rand(0..100)/100:
for k to 25 do
p:=rd()*z^250+randpoly(z,degree=250,terms=3)+rd();
r:=fsolve(p=0,z,complex);
L[k]:=complexplot([r],style=point,symbol=circle,color=COLOR(RGB,rc(),rc(),rc()),
scaling=constrained,caption=typeset("Rødderne i ",p));
end do:
display(seq(L[k],k=1..25),insequence=true);
Differentialligning af 2. orden
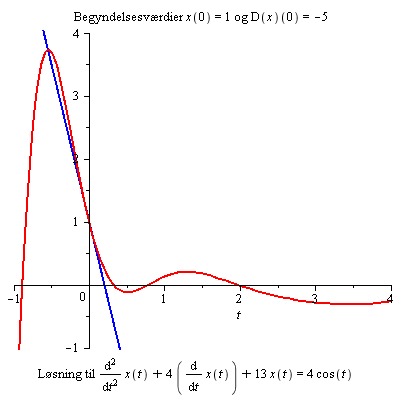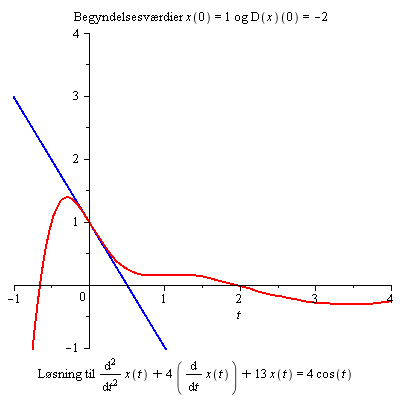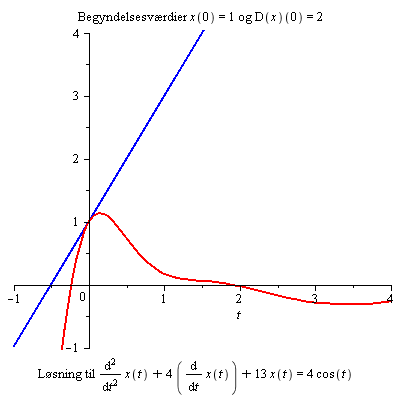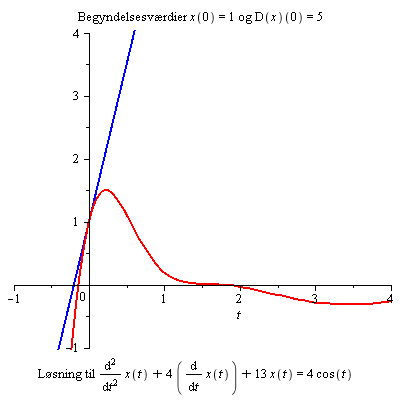
Forklar, hvorfor ændring af begyndelsesbetingelserne ikke har nogen synderlig virkning for t > 3.
Maple-kommandoerne
with(plots):
ligningi:=diff(x(t),t,t)+4*diff(x(t),t)+13*x(t)=4*cos(t):
res:=dsolve({ligningi,x(0)=1,D(x)(0)=a}):
f:=unapply(subs(res,x(t)),t):
tangent:=f(0)+D(f)(0)*t:
r1:=-1..4: r2:=-1..4:
p1:=animate(plot,[tangent,t=r1,r2,color=blue, thickness=2,
title=typeset("Begyndelsesværdier ",x(0) = 1," og ", D(x)(0)=a)],
a=[seq(k,k=-5..5)],paraminfo=false):
p2:=animate(plot,[f(t),t=r1,r2, thickness=2],a=[seq(k,k=-5..5)],paraminfo=false):
display(p1,p2,caption=typeset("Løsning til ",ligningi));
Differentialligning af 2. orden (udgave 2)
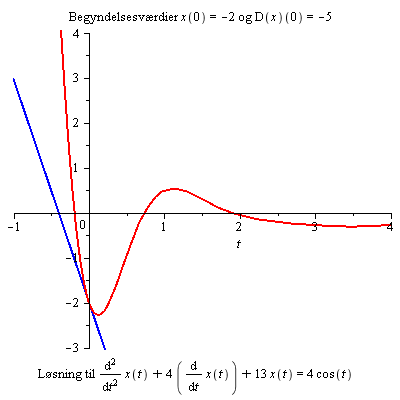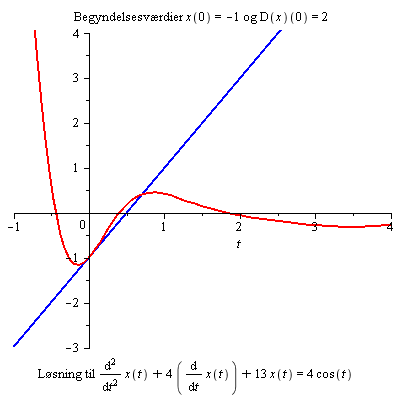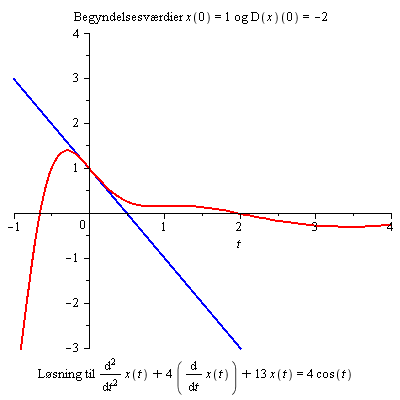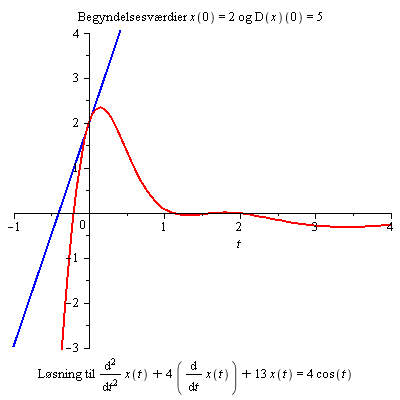
Ændringerne i begyndelsesbetingelserne synes ikke ikke at have nogen synderlig virkning for t > 3. Hvorfor?
Maple-kommandoerne
Hver af de to animationer er dobbeltanimationer: animate animerer animate!
with(plots):
ligningi:=diff(x(t),t,t)+4*diff(x(t),t)+13*x(t)=4*cos(t):
res:=dsolve({ligningi,x(0)=x0,D(x)(0)=x1}):
f:=unapply(subs(res,x(t)),t):
tangent:=f(0)+D(f)(0)*t:
r1:=-1..4: r2:=-3..4:
p1:=animate(animate,[plot,[tangent,t=r1,r2,color=blue, thickness=2,
title=typeset("Begyndelsesværdier ",x(0) = x0," og ", D(x)(0)=x1)],
x1=[seq(k,k=-5..5)],paraminfo=false],x0=[seq(k,k=-2..2)],paraminfo=false):
p2:=animate(animate,[plot,[f(t),t=r1,r2, thickness=2],x1=[seq(k,k=-5..5)],paraminfo=false],
x0=[seq(k,k=-2..2)],paraminfo=false):
display(p1,p2,caption=typeset("Løsning til ",ligningi));
Farver
Maple-kommandoerne
Her er brugt MultiAnimate fra DMat-pakken sammen med RGBtoHEX fra samme pakke.
MultiAnimate(plot,[1,0..1,0..1,color=COLOR(RGB,rød,grøn,blå),filled=true,
axes=none,caption=cat("HEX-værdien for farven: ",RGBtoHEX([rød,grøn,blå]))],
[blå=0..1.,grøn=0..1.,rød=0..1.]);
Farver, version 2

Denne version springer med samme farveafstand fra billede til billede.
Maple-kommandoerne
with(plots,display):
with(DMat):
N:=6:s1:=1: s2:=1:
L:=NULL:
for k3 from 0 to N do
for k2 from 0 to N do
for k1 from 0 to N do
L:=L,[k3,s2*k2+(1-s2)*(N-k2),s1*k1+(1-s1)*(N-k1)];
if k1=N then s1:=1-s1 end if;
end do;
if k2=N then s2:=1-s2 end if;
end do
end do;
L1:=evalf(map(x->x/N,[L])):
B:=NULL:
for k from 1 to nops(L1) do
TF:=TaettesteFarve(L1[k],vis=false,outputformat=hex);
B:=B,plot(1,0..1,0..1,filled=true,axes=none,color=COLOR(RGB,op(L1[k])),
caption=cat("HEX-værdien for farven: ",RGBtoHEX(L1[k])," \nTætteste farve med engelsk html-navn:\n",TF[1]," ",TF[2]),
title=typeset(RGB(op(Chop(L1[k],3)))) )
end do:
display(B,insequence=true);
Animation i Blåt
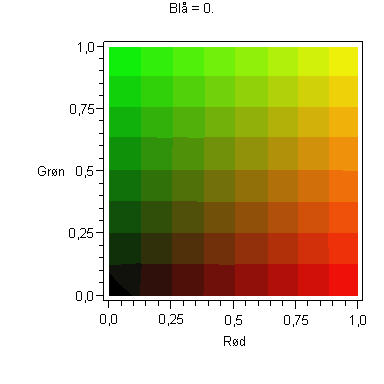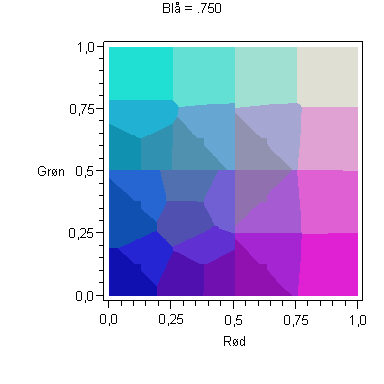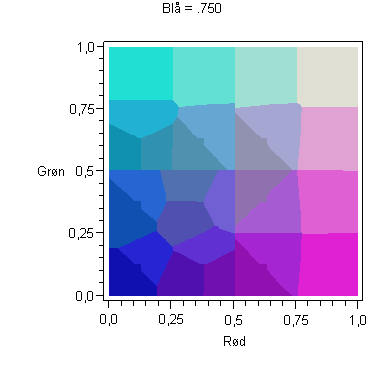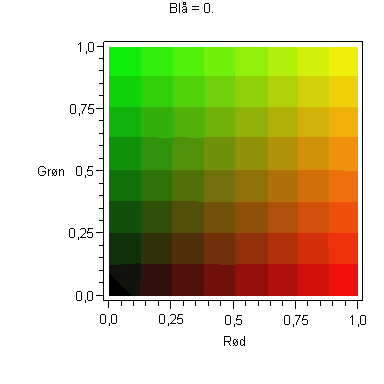
Maple-kommandoerne
with(plots,animate):
with(DMat,Chop):
cs:=x->convert(Chop((1+sin(x))/2,3),string):
animate(plot3d,[0,R=0..1,G=0..1,style=patchnogrid,orientation=[-90,0],
axes=boxed,labels=["Rød","Grøn",""],color=COLOR(RGB,R,G,(1+sin(x))/2),
title=cat("Blå = ",'cs(x)')],
x=-Pi/2..3*Pi/2,paraminfo=false,frames=100);
Lorenz- rutschebanen
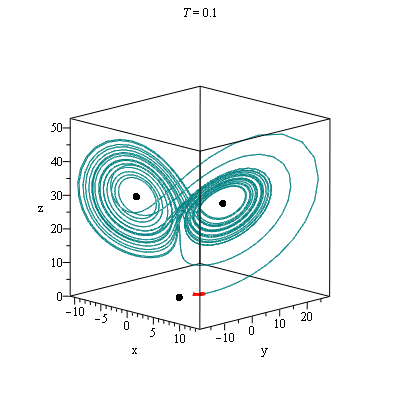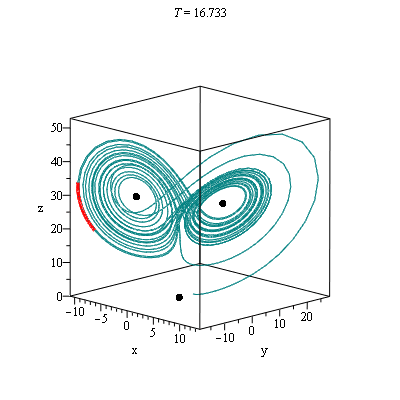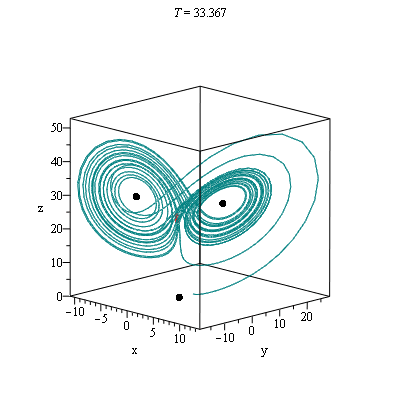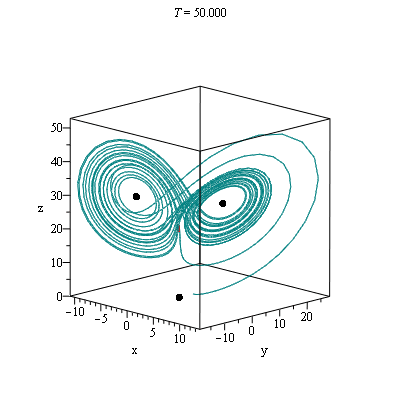
Maple-kommandoerne
with(plots):
f:=(x,y,z)->sigma*(y-x);
g:=(x,y,z)->rho*x-y-x*z;
h:=(x,y,z)->-beta*z+x*y;
lorenz:={diff(x(t),t)=f(x(t),y(t),z(t)),diff(y(t),t)=g(x(t),y(t),z(t)),diff(z(t),t)=h(x(t),y(t),z(t))};
#Ligevægtspunkter:
_EnvExplicit:=true:
solve({f(x,y,z)=0,g(x,y,z)=0,h(x,y,z)=0},{x,y,z});
pkt:=map(subs,[%],[x,y,z]);
#Vi vælger følgende konkrete parameterværdier til brug ved illustrationen nedenfor.
param:={sigma=3,beta=1,rho=30};
#Begyndelsesbetingelser:
begbet:={x(0)=0,y(0)=5,z(0)=0}:
T0:=50:
L:=dsolve(subs(param,lorenz) union begbet,
{x(t),y(t),z(t)},type=numeric,output=listprocedure,range=0..T0):
lp:=pointplot3d(subs(param,pkt),symbol=solidsphere,symbolsize=20,color=black):
baggrund:=display(odeplot(L,[x(t),y(t),z(t)],0..T0,numpoints=2000,axes=boxed,color="Teal"),lp):
animate(odeplot,[L,[x(t),y(t),z(t)],T-.1..T,axes=boxed,thickness=3,orientation=[-45,75]],T=0.1..T0,frames=400,background=baggrund);
arkiv.php
Sidst ændret: 08.08.2010 kl 13:01:39
|